HashMap分析
hash函数
// 1.7
static int hash(int h) {
h ^= (h >>> 20) ^ (h >>> 12);
return h ^ (h >>> 7) ^ (h >>> 4);
}
// 1.8
static final int hash(Object key) {
int h;
return (key == null) ? 0 : (h = key.hashCode()) ^ (h >>> 16);
}
这个函数也叫扰动函数,它的作用就是解决hash冲突的。
indexFor函数
获取hash时真正的索引值。这个函数也叫索引函数
static int indexFor(int hash, int length) {
return hash & (length-1);
}
扰动函数和索引函数的作用
索引函数的作用就是实际的找到value值存储的位置,这里的运算是“与”运算,这个的效率更高,相对于“取模”运算,这个的运算消耗更小。
这里是hash数组的length-1,这个正好是数组的实际容纳容量,并且由于数组的大小都是2的指数,减1能在地位产生更多的1,正好相当于一个低位掩码
那扰动函数的作用是啥?
由于“与”操作的结果是高位全部归零,只保留了低位的值。这样的问题就来了,由于不管我的h值是怎样的,最后只取最低的几位(由数组的大小决定),这样碰撞还是很严重的。更要命的是如果散列本身做得不好,分布上成等差数列的漏洞,恰好使最后几个低位呈现规律性重复,就无比蛋疼。
hash函数的输入值是int,如果啥都不做的话,基本也是可以用的,因为int值的范围从-2147483648到2147483648,但是由于与操作的问题,需要加入扰动函数。
1.7和1.8的扰动函数有所不同,但是它们的目的是一样的,1.8更加的简单化。就是混淆原始哈希码的高位和地位,以此来加大低位的随机性,或者说低位的值也反映了高位的特征,高位的信息被变相的保留下来,而不担心后面与操作直接被忽略调
以1.8为例:
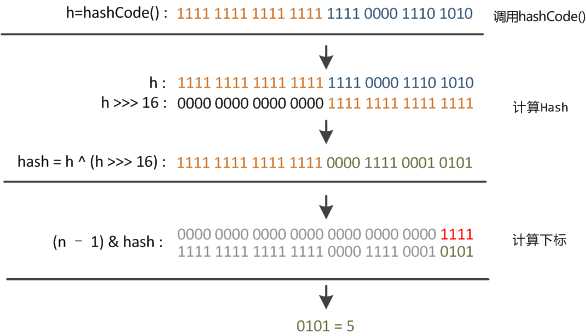
扰动函数的效果怎么样呢?
随机选取了352个字符串,在他们散列值完全没有冲突的前提下,对它们做低位掩码,取数组下标。
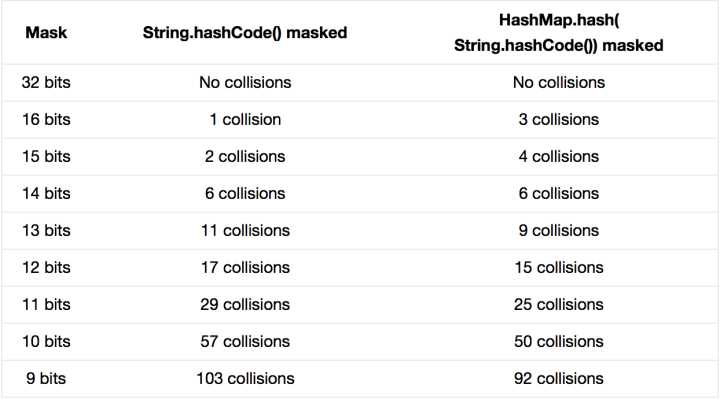
可以看出,随着掩码位数的减少,扰动函数的作用就更为明显。
构造
hashmap提供了多种构造方法,这里主要分析:
// 1.7
public HashMap(Map<? extends K, ? extends V> m) {
this(Math.max((int) (m.size() / DEFAULT_LOAD_FACTOR) + 1,
DEFAULT_INITIAL_CAPACITY), DEFAULT_LOAD_FACTOR);
putAllForCreate(m);
}
// 1.8
public HashMap(Map<? extends K, ? extends V> m) {
this.loadFactor = DEFAULT_LOAD_FACTOR;
putMapEntries(m, false);
}
Entry结构体
// 1.7
static class Entry<K,V> implements Map.Entry<K,V> {
final K key;
V value;
Entry<K,V> next;
final int hash;
...
}
// 1.8
static class Node<K,V> implements Map.Entry<K,V> {
final int hash;
final K key;
V value;
Node<K,V> next;
...
}
从上面看,1.7和1.8没有什么差异,都是一个链的概念。
Resize计算
1.7的大小计算:
void resize(int newCapacity) {
Entry[] oldTable = table;
int oldCapacity = oldTable.length;
if (oldCapacity == MAXIMUM_CAPACITY) {
threshold = Integer.MAX_VALUE;
return;
}
Entry[] newTable = new Entry[newCapacity];
transfer(newTable);
table = newTable;
threshold = (int)(newCapacity * loadFactor);
}
/**
* Transfers all entries from current table to newTable.
*/
void transfer(Entry[] newTable) {
Entry[] src = table;
int newCapacity = newTable.length;
for (int j = 0; j < src.length; j++) {
Entry<K,V> e = src[j];
if (e != null) {
src[j] = null;
do {
Entry<K,V> next = e.next;
int i = indexFor(e.hash, newCapacity);
e.next = newTable[i];
newTable[i] = e;
e = next;
} while (e != null);
}
}
}
1.7的resize就是把数组变大,计算就是原始容量乘上加载因子loadFactor;然后将原来的table里的数据放入到新的数组里。
1.8的大小计算
final Node<K,V>[] resize() {
Node<K,V>[] oldTab = table;
int oldCap = (oldTab == null) ? 0 : oldTab.length;
int oldThr = threshold;
int newCap, newThr = 0;
if (oldCap > 0) {
if (oldCap >= MAXIMUM_CAPACITY) {
threshold = Integer.MAX_VALUE;
return oldTab;
}
else if ((newCap = oldCap << 1) < MAXIMUM_CAPACITY &&
oldCap >= DEFAULT_INITIAL_CAPACITY)
newThr = oldThr << 1; // 直接增大2倍
}
else if (oldThr > 0) // 设定了初始的threshold
newCap = oldThr;
else { // 初始化容量
newCap = DEFAULT_INITIAL_CAPACITY;
newThr = (int)(DEFAULT_LOAD_FACTOR * DEFAULT_INITIAL_CAPACITY);
}
// 类似1.7的容量大小增长
if (newThr == 0) {
float ft = (float)newCap * loadFactor;
newThr = (newCap < MAXIMUM_CAPACITY && ft < (float)MAXIMUM_CAPACITY ?
(int)ft : Integer.MAX_VALUE);
}
threshold = newThr;
Node<K,V>[] newTab = (Node<K,V>[])new Node[newCap];
table = newTab;
if (oldTab != null) {
// 红黑树操作
... ...
}
return newTab;
}
可以看出,1.8的容量扩充更为复杂,分3种情况:
- 通过空的构造体实例化的hashmap,没有任何的数据,则直接初始化容量
- 已经有了数据,则直接扩大2倍
- 没有数据,但是threshold已经设置了值,则按1.7的增长算法进行扩容
在扩容后,数据是通过红黑树的方式添加到新的数组中的。
冲突处理(基于1.7)
1.7的内部存储结构采用的是数组和链表的结合。
链表的出现主要是为了解决hash地址冲突的问题。
// 储存 key-value 键值对的数组,一个键值对对象映射一个Entry对象
transient Entry[] table;
具体实现
系统总是将新添加的Entry对象放入table数组的bucketIndex索引处——如果 bucketIndex 索引处已经有了一个 Entry 对象,那新添加的 Entry 对象指向原有的 Entry 对象(产生一个 Entry 链),如果 bucketIndex 索引处没有 Entry 对象,也就是上面程序代码的 e 变量是 null,也就是新放入的 Entry 对象指向 null,也就是没有产生 Entry 链。

存在的性能问题
HashMap里面没有出现hash冲突时,没有形成单链表时,hashmap查找元素很快,查询时间为O(1);get()方法能够直接定位到元素,但是出现单链表后,单个bucket 里存储的不是一个 Entry,而是一个 Entry 链,系统只能必须按顺序遍历每个 Entry,直到找到想搜索的 Entry 为止——如果恰好要搜索的 Entry 位于该 Entry 链的最末端(该 Entry 是最早放入该 bucket 中),那系统必须循环到最后才能找到该元素,这时时间消耗为O(N)。这就是链表解决冲突后出现的问题。
1.8的优化处理
1.8对上面问题提出了解决方案,就是在链表的基础上采用红黑树的方式。具体看HashMap java 8分析
补充知识 - hashmap冲突的处理方式
- 开放地址法,即再散列
- 链地址法
- 伪随机数
存储
1.7和1.8的存储逻辑基本一样:
- 获取key的hashcode
- 二次hash
- 通过hash找到对应的index
- 插入链表
public V put(K key, V value) {
if (key == null)
return putForNullKey(value);
int hash = hash(key.hashCode());
int i = indexFor(hash, table.length);
for (Entry<K,V> e = table[i]; e != null; e = e.next) {
Object k;
if (e.hash == hash && ((k = e.key) == key || key.equals(k))) {
V oldValue = e.value;
e.value = value;
e.recordAccess(this);
return oldValue;
}
}
modCount++;
addEntry(hash, key, value, i);
return null;
}
void addEntry(int hash, K key, V value, int bucketIndex) {
Entry<K,V> e = table[bucketIndex];
table[bucketIndex] = new Entry<>(hash, key, value, e);
if (size++ >= threshold)
resize(2 * table.length);
}
读取
- bucket里的第一个节点,直接命中;
- 如果有冲突,则通过key.equals(k)去查找对应的entry
- 若为树(1.8),则在树中通过key.equals(k)查找,O(logn);
- 若为链表(1.7),则在链表中通过key.equals(k)查找,O(n)。
public V get(Object key) {
if (key == null)
return getForNullKey();
int hash = hash(key.hashCode());
for (Entry<K,V> e = table[indexFor(hash, table.length)];
e != null;
e = e.next) {
Object k;
if (e.hash == hash && ((k = e.key) == key || key.equals(k)))
return e.value;
}
return null;
}